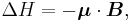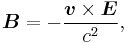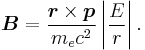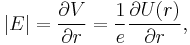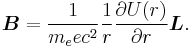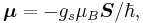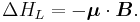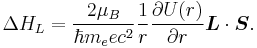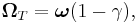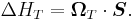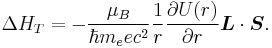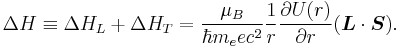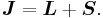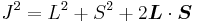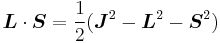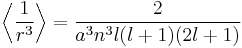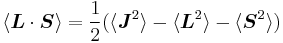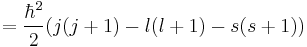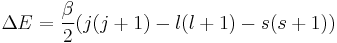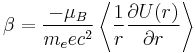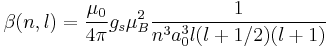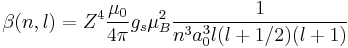Spin–orbit interaction

In quantum physics, the spin–orbit interaction (also called spin–orbit effect or spin–orbit coupling) is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and the nucleus's magnetic field. This is detectable as a splitting of spectral lines. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin-orbit effects for electrons in semiconductors and other materials are explored and put to useful work.

1 Spin–orbit interaction in atomic energy levels
2 See also
3 References
4 Textbooks

Spin–orbit interaction in atomic energy levels

Using some semiclassical electrodynamics and non-relativistic quantum mechanics, in this section we present a relatively simple and quantitative description of the spin-orbit interaction for an electron bound to an atom, up to first order in perturbation theory. This gives results that agree reasonably well with observations. A more rigorous derivation of the same result would start with the Dirac equation, and achieving a more precise result would involve calculating small corrections from quantum electrodynamics.

Energy of a magnetic moment

The energy of a magnetic moment in a magnetic field is given by:

$\Delta H=-\boldsymbol{\mu}\cdot\boldsymbol{B},$

where μ is the magnetic moment of the particle and B is the magnetic field it experiences.

Magnetic field

We shall deal with the magnetic field first. Although in the rest frame of the nucleus, there is no magnetic field, there is one in the rest frame of the electron. Ignoring for now that this frame is not inertial, in SI units we end up with the equation

$\boldsymbol{B} = - {\boldsymbol{v} \times \boldsymbol{E}\over c^2},$

where v is the velocity of the electron and E the electric field it travels through. Now we know that E is radial so we can rewrite 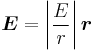$\boldsymbol{E} =\left | {E\over r}\right| \boldsymbol{r}$ . Also we know that the momentum of the electron 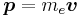$\boldsymbol{p} =m_e \boldsymbol{v}$ . Substituting this in and changing the order of the cross product gives:

$\boldsymbol{B} = {\boldsymbol{r}\times\boldsymbol{p}\over m_ec^2} \left | {E\over r}\right|.$

Next, we express the electric field as the gradient of the electric potential 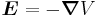$\boldsymbol{E} = -\boldsymbol{\nabla}V$ . Here we make the central field approximation, that is, that the electrostatic potential is spherically symmetric, so is only a function of radius. This approximation is exact for hydrogen, and indeed hydrogen-like systems. Now we can say

$\left | E\right| = {\partial V \over \partial r}={1\over e}{\partial U(r) \over \partial r},$

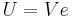where $U=Ve$ is the potential energy of the electron in the central field, and e is the elementary charge. Now we remember from classical mechanics that the angular momentum of a particle 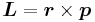$\boldsymbol{L} = \boldsymbol{r}\times\boldsymbol{p}$ . Putting it all together we get

$\boldsymbol{B} = {1\over m_eec^2}{1\over r}{\partial U(r) \over \partial r} \boldsymbol{L}.$

It is important to note at this point that B is a positive number multiplied by L, meaning that the magnetic field is parallel to the orbital angular momentum of the particle.

Magnetic Moment of the Electron

The magnetic moment of the electron is

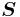$\boldsymbol{\mu} = -g_s\mu_B\boldsymbol{S}/ \hbar,$

where $\boldsymbol{S}$ is the spin angular momentum vector, 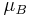$\mu_B$ is the Bohr magneton and 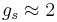$g_s\approx 2$ is the electron spin g-factor. Here, 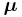$\boldsymbol{\mu}$ is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum.

The spin-orbit potential consists of two parts. The Larmor part is connected to interaction of the magnetic moment of electron with magnetic field of nucleus in the co-moving frame of electron. The second contribution is related to Thomas precession.

Larmor interaction energy

The Larmor interaction energy is

$\Delta H_{L} =-\boldsymbol{\mu}\cdot\boldsymbol{B}.$

Substituting in this equation expressions for the magnetic moment and the magnetic field, one gets

$\Delta H_{L} = {2\mu_B\over \hbar m_e e c^2}{1\over r}{\partial U(r) \over \partial r} \boldsymbol{L}\cdot\boldsymbol{S}.$

Now, we have to take into account Thomas precession correction for the electron's curved trajectory.

Thomas interaction energy

In 1926 Llewellyn Thomas relativistically recomputed the doublet separation in the fine structure of the atom.^[1]. Thomas precession rate, 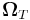$\boldsymbol{\Omega}_T$ , is related to the angular frequency of the orbital motion, 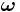$\boldsymbol{\omega}$ , of a spinning particle as follows ^[2]^[3]

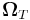$\boldsymbol{\Omega}_T = \boldsymbol{\omega} (1 - \gamma),$

where $\gamma$ is the Lorentz factor of moving particle. The Hamiltonian producing the spin precession $\boldsymbol{\Omega}_T$ is given by

$\Delta H_{T} = \boldsymbol{\Omega}_T \cdot \boldsymbol{S}.$

To the first order in 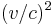$(v/c)^2$ , we obtain

$\Delta H_{T} = - {\mu_B\over \hbar m_e e c^2}{1\over r}{\partial U(r) \over \partial r} \boldsymbol{L}\cdot\boldsymbol{S}.$

Total interaction energy

The total spin-orbit potential in an external electrostatic potential takes the form

$\Delta H \equiv \Delta H_{L} %2B \Delta H_{T} = {\mu_B\over \hbar m_e e c^2}{1\over r}{\partial U(r) \over \partial r} (\boldsymbol{L}\cdot\boldsymbol{S}).$

The net effect of Thomas precession is the reduction of the Larmor interaction energy by factor 1/2 which came to be known as the Thomas half.

Evaluating the energy shift

Thanks to all the above approximations, we can now evaluate the detailed energy shift in this model. In particular, we wish to find a basis that diagonalizes both H₀ (the non-perturbed Hamiltonian) and ΔH. To find out what basis this is, we first define the total angular momentum operator

$\boldsymbol{J}=\boldsymbol{L}%2B\boldsymbol{S}.$

Taking the dot product of this with itself, we get

$J^2=L^2%2BS^2%2B2\boldsymbol{L}\cdot \boldsymbol{S}$

(since L and S commute), and therefore

$\boldsymbol{L}\cdot\boldsymbol{S}= {1\over 2}(\boldsymbol{J}^2 - \boldsymbol{L}^2 - \boldsymbol{S}^2)$

It can be shown that the five operators H₀, J², L², S², and J_z all commute with each other and with ΔH. Therefore, the basis we were looking for is the simultaneous eigenbasis of these five operators (i.e., the basis where all five are diagonal). Elements of this basis have the five quantum numbers: n (the "principal quantum number") j (the "total angular momentum quantum number"), l (the "orbital angular momentum quantum number"), s (the "spin quantum number"), and j_z (the "z-component of total angular momentum").

To evaluate the energies, we note that

$\left \langle {1\over r^3} \right \rangle = \frac{2}{a^3 n^3 l(l%2B1)(2l%2B1)}$

for hydrogenic wavefunctions (here 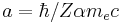$a = \hbar / Z \alpha m_e c$ is the Bohr radius divided by the nuclear charge Z); and

$\left \langle \boldsymbol{L}\cdot\boldsymbol{S} \right \rangle={1\over 2}(\langle\boldsymbol{J}^2\rangle - \langle\boldsymbol{L}^2\rangle - \langle\boldsymbol{S}^2\rangle)$

$={\hbar^2\over 2}(j(j%2B1) - l(l%2B1) -s(s%2B1))$

Final Energy Shift

We can now say

$\Delta E = {\beta\over 2}(j(j%2B1) - l(l%2B1) -s(s%2B1))$

where

$\beta = {-\mu_B\over m_eec^2}\left\langle{1\over r}{\partial U(r) \over \partial r}\right\rangle$

For hydrogen, we can write the explicit result

$\beta (n,l) = {\mu_0\over 4\pi}g_s\mu_B^2{1\over n^3a_0^3l(l%2B1/2)(l%2B1)}$

For any hydrogen-like atom with Z protons

$\beta (n,l) = Z^4{\mu_0\over 4\pi}g_s\mu_B^2{1\over n^3a_0^3l(l%2B1/2)(l%2B1)}$

References

^ L. H. Thomas, The motion of the spinning electron, Nature (London), 117, 514 (1926).
^ L. Föppl and P. J. Daniell, Zur Kinematik des Born'schen starren Körpers, Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 519 (1913).
^ C. Møller, The Theory of Relativity, (Oxford at the Claredon Press, London, 1952).

Textbooks

E. U. Condon and G. H. Shortley (1935). The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4.

D. J. Griffiths (2004). Introduction to Quantum Mechanics (2nd edition). Prentice Hall.

Landau, Lev; L. M. Lifshitz. " $\S$ 72. Fine structure of atomic levels". Quantum Mechanics: Non-Relativistic Theory, Volume 3.

Spin–orbit interaction

Contents